
Perhaps
the Easiest Method of Building a Database Response Model
Bruce Ratner, Ph.D.
The purpose of this
article is to present a new method – the GenIQ Model© – as an
alternative technique for modeling a response variable. For ease of
presentation, I use two categorical and two continuous variables, and a
binary (yes-no) target variable. The GenIQ Model, which is based on the
assumption-free, nonparametric genetic paradigm inspired by Darwin’s
Principle of Survival of the Fittest, offers theoretical and
ease-of-use advantages over the standard logistic regression model
(LRM) and the log-linear model (LLM). It automatically and
simultaneously “evolves” the response model structure, and the variable
selection among categorical predictor variables. The open-worked GenIQ
Model and its wordbook are both generally regarded as not demanding on
newcomers of genetic modeling. A novel case study using the “Let’s
Play” dataset is illustrated to encourage the use of the new method.
I use the machine
learning GenIQ Model to build a database response model, which predicts
the rank-order likelihood of response, to illustrate the advantages,
and to highlight the singular weakness of the machine learning
paradigm. Specifically, the GenIQ Model shows the superiority of the
machine learning paradigm over the statistical paradigm, as it not only
specifies the true model form (a computer program), but simultaneously
performs variable selection, data mining and build the model – it’s
like a Genetic Jackknife 3-in-1 Method. The difficulty in interpreting
the computer program often accounts for the limited use of the machine
learning paradigm.
For a preview of the 9-step modeling process of GenIQ, click here. For FAQs about GenIQ, click here.
For a preview of the 9-step modeling process of GenIQ, click here. For FAQs about GenIQ, click here.
Outline
of Article
I. Situation
When my daughter Amanda
was in grade school, she could not understand the decision-making
process of her principal Dr. Katz. On some rainy days, Dr. Katz would
permit the class to go outside for recess to play. On other days when
it was sunny, Dr. Katz would said, “no play.” As a statistician’s
daughter, Amanda collected some weather information, and asked me to
build a model to predict what Dr. Katz will do in the days to come.
Amanda created a “Let’s Play” database, in Table 1 (also in Quinlan’s
C4.5, page 18!), which included the weather conditions for two weeks:
1. Outlook (sunny, rainy, overcast)
2. Temperature
3. Humidity
4. Windy (yes, no), and of course
5. Play (yes, no).
I built the
easy-to-interpret LRM, and the not-so-easy-to-interpret GenIQ Model for
the target variable Play (yes). This creates a counterpoint where the
data analyst now can choose between a good interpretable model and a
potentially better unexplainable model.

II. LRM Output
The LRM output (Analysis of Maximum Likelihood Estimates) - arguably the best Play-LRM equation (model) is below.
(Log of odds of) Play (yes) =
11.7403 - 2.2682*Outlook(sunny) - 0.1124*Humidity - 2.0470*Windy(yes)
III. Play-LRM Results
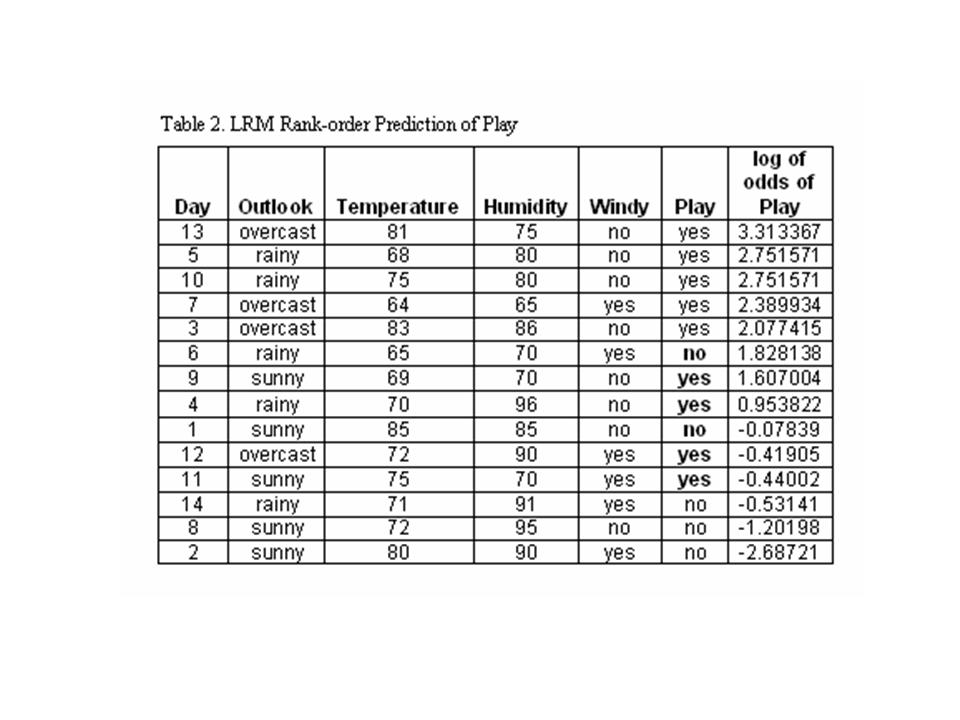
The results of the Play-LRM are in Table 2. There is not a perfect rank-order prediction of Play for days 6, 1, 12 and 11.
IV. GenIQ Model Output
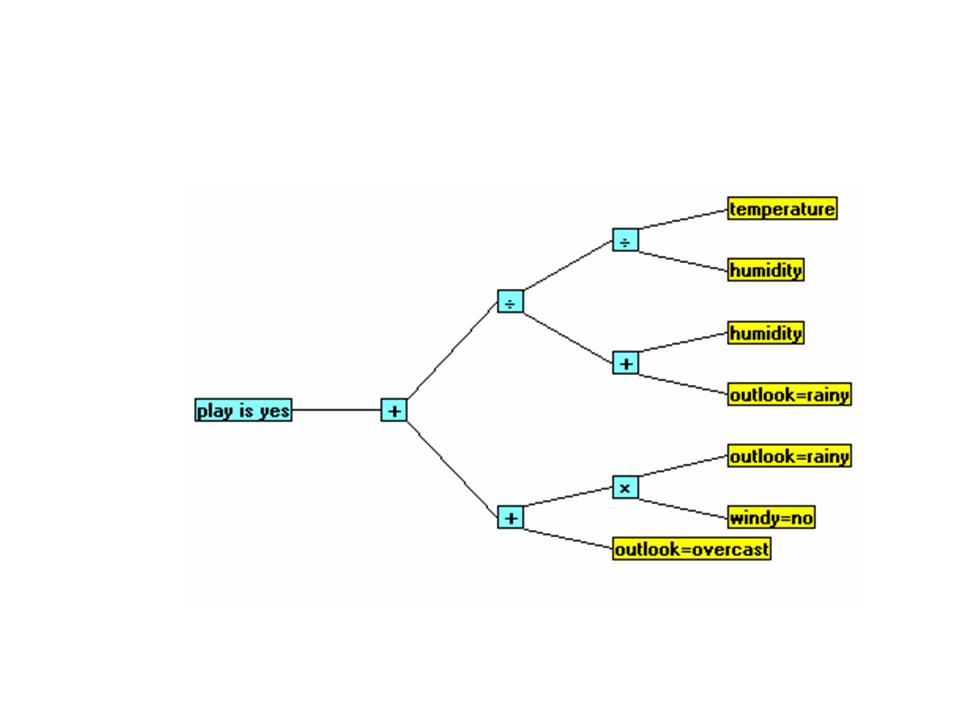
The Play-GenIQ Model tree display and its form (computer program) are below.
The GenIQ Model
(Tree Display)
The
GenIQ Model (Code)
If outlook = "overcast" Then x1 = 1; Else x1 = 0;
If windy = "no" Then x2 = 1; Else x2 = 0;
If outlook = "rainy" Then x3 = 1; Else x3 = 0;
x2 = x2 * x3;
x1 = x1 + x2;
If outlook = "rainy" Then x2 = 1; Else x2 = 0;
x3 = humidity;
x2 = x2 + x3;
x3 = humidity;
x4 = temperature;
If x3 NE 0 Then x3 = x4 / x3; Else x3 = 1;
If x2 NE 0 Then x2 = x3 / x2; Else x2 = 1;
x1 = x1 + x2;
GenIQvar = x1;
V. GenIQ Variable Selection
GenIQ variable
selection provides a rank-ordering of variable importance for a
predictor variable with respect to other predictor variables considered
jointly. This is in stark contrast to the well-known, always-used
statistical correlation coefficient, which only provides a simple
correlation between a predictor variable and the target variable -
independent of the other predictor variables under consideration.
Variable Importance (w/r/to other variables considered jointly)
1. Outlook (overcast)
2. Outlook (rainy)
3. Windy (no)
4. Humidity
5. Outlook (sunny)
6. Windy (yes)
7. Temperature
VI. GenIQ Data Mining
GenIQ data mining is
directly apparent from the GenIQ tree itself: Each branch is a newly
constructed variable, which has power to increase the rank-order
predictions.
1. Var1 = Temperature / Humidity
2. Var2 = Humidity + Outlook (rainy)
3. Var3 = Var1 / Var2
4. Var4 = Outlook (rainy) * Windy (no)
5. Var5 = Var4 / Outlook (overcast)
6. GenIQ Model = Var3 / Var5
VII. Play-GenIQ Model Results
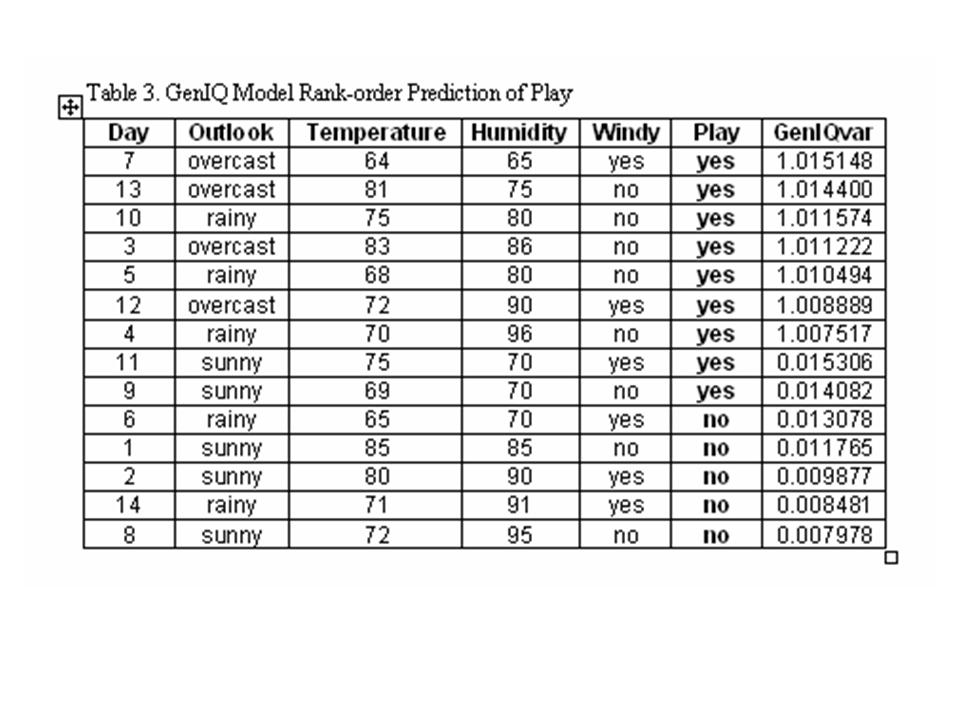
The results of the Play-GenIQ Model are in Table 3. There is a perfect rank-order prediction of Play.
VIII. Summary
The machine learning
paradigm (MLP) “let the data suggest the model” is a practical
alternative to the statistical paradigm “fit the data to
the equation,” which has its roots when data were only “small.” It
was – and still is – reasonable to fit small data in a rigid
parametric, assumption-filled model. However, the current information
(big data) in, say, cyberspace requires a paradigm shift. MLP is a
utile approach for database response modeling when dealing with big
data, as big data can be difficult to fit in a specified model. Thus,
MLP can function alongside the regnant statistical approach when the
data – big or small – simply do not “fit.” As demonstrated with the
“Let’s Play” data, MLP works well within small data settings.
Go to Software page.
1 800 DM STAT-1; or e-mail at br@dmstat1.com.